সাহিত্য ডট্ অৰ্গত প্ৰকাশিত (অক্টোবৰ, ২০২১)
চিন্তা কৰিব পৰা মেছিনসমূহ
কৃটিম বুদ্ধিমত্তা বুলি ক'লে পোনেই আৰ্থাৰ ছি ক্লাৰ্কৰ হাল-৯০০০ বা টাৰ্মিনেটৰ চিনেমাখনৰ স্কাইনেটৰ দৰে চৰিত্ৰবোৰলৈ মনত পৰে। কল্পবিজ্ঞানৰ বাবে প্ৰয়োজনীয় অতিৰঞ্জিত কথাখিনি আঁতৰাই চালে কিন্তু এয়া কোনো অদ্ভুত বস্তু নহয়, বৰঞ্চ কম্পিউটাৰ বিজ্ঞানৰ সহায়ত অতি চতুৰ পদ্ধতিৰে ৰৈখিক পাটিগণিতৰ দৰে সৰল বিষয়ৰ সহায় লৈ কৰা কিছুমান গণনাৰ ফলাফলহে। আজিৰ দিনত আমি অনুভৱ নকৰাকৈয়ে আমাৰ চৌদিশে মানৱ মস্তিষ্কৰ দৰেই তথ্য বিশ্লেষণ কৰি চিন্তা কৰিব পৰা কম্পিউটাৰ প্ৰগ্ৰেমৰে ভৰি আছে। নহ'লেনো আপুনি অনলাইন বজাৰত মনে প্ৰাণে বিচাৰি থকা বস্তুটোৰ বিজ্ঞাপন ইউটিউব বা ফেচবুকে নিজৰ ৱেবপেজটোত দেখুৱাব লাগে বুলি কেনেকৈ শিকিলে? আপুনি টাইপ কৰা কেইটামান শব্দৰ ওপৰত ভিত্তি কৰি পৰৱৰ্তী শব্দকেইটা কি হ'ব সেয়া গুগল ৱেবছাইটটোৱে কেনেকৈ শিকিলে? আপোনাৰ ক্লাউড ষ্ট'ৰেজৰ ফটোবোৰত থকা ব্যক্তিকেইজনক আপোনাৰ ফোনটোৱে চিনাক্ত কৰি পৃথককৈ ৰাখিবলৈ কেনেকৈ শিকিলে? মানুহৰ মস্তিষ্কৰ তুলনাত কম্পিউটাৰৰ এইধৰণৰ চিন্তা কৰি সিদ্ধান্ত ল'ব পৰা ক্ষমতাসমূহ এতিয়াও অতি চালুকীয়া অৱস্থাতে আছে যদিও সমগ্ৰ প্ৰণালীটোৰ মূল নীতি একেই।

কৃটিম বুদ্ধিমত্তাৰ প্ৰাৰম্ভিক ধাৰণাসমূহৰ কাহিনীটোৰ আৰম্ভণি হয় দ্বিতীয় বিশ্বযুদ্ধৰ সময়ৰ এজন অগতানুগতিক ইংৰাজ গণিতজ্ঞ এলেন টিউৰিং আৰু এনিগ্মা (Enigma) নামৰ এটা জাৰ্মান যন্ত্ৰৰ পৰা। এই বিশেষ যন্ত্ৰটোৰ সহায় লৈ জাৰ্মান সৈন্যই গোপন বাৰ্তাসমূহক বেবেৰিবাং আখৰৰ সমষ্টিলৈ ৰূপান্তৰিত কৰি আনলৈ প্ৰেৰণ কৰিছিল, আৰু সেই বাৰ্তা লাভ কৰা ব্যক্তিজনেও একেই যন্ত্ৰৰ সহায়ত বেবেৰিবাং বাৰ্তাটোক পুনৰ অৰ্থৱহ জাৰ্মান বাৰ্তালৈ ৰূপান্তৰিত কৰিছিল। ইংৰাজসকলে চোৰাংকৈ এনে এটা যন্ত্ৰ গোটাবলৈ সক্ষম হৈছিল যদিও ইয়াৰ স্ক্ৰু-আৰু বুতামবোৰৰ প্ৰায় ১৫ হাজাৰ কোটি বিন্যাসৰ মাজৰ কোনটো বিশেষ বিন্যাসে সেই বেবেৰিবাং বাৰ্তাটোক পঢ়িব পৰা কৰি তুলিব সেয়া নজনাৰ বাবে সেইটোক ব্যৱহাৰ কৰিব পৰা হোৱা নাছিল। অতি চালাক জাৰ্মানসকলে সেই বিশেষ বিন্যাসটো প্ৰতিদিনেই সলনি কৰিছিল, যাতে কোনোবাই কেতিয়াবা কাকতালীয়ভাৱে শুদ্ধ বিন্যাসটো অনুমান কৰিলেও তেওঁ পিছদিনাৰ বাৰ্তাখিনি পঢ়িব নোৱাৰে। অৰ্থাৎ এই এনিগ্মা আছিল এক অসম্ভৱ সাঁথৰ। সেয়েহে ইংৰাজ চোৰাংচোৱা বিভাগ MI-6 এ বেবেৰিবাং জাৰ্মান বাৰ্তাৰ মাজত পেটাৰ্ণ বিছাৰি বাৰ্তাসমূহ decrypt কৰাৰ বাবে দেশখনৰ অতি চোকা গণিতজ্ঞ কেইজনমানক বাছনি কৰিছিল। এই গণিতজ্ঞ সকলৰেই মাজত অন্যতম এজন আছিল এলেন টিউৰিং। অৱশ্যে পৃথিৱীৰ আটাইতকৈ চোকা গণিতজ্ঞ জনৰ বাবেও এদিনৰ ভিতৰত সেই ১৫ কোটি প্ৰকাৰৰ বিশৃংখলতাৰ মাজৰ পৰা সঠিক প্ৰকাৰৰ বিশৃংখলতাটো বিছাৰি উলিওৱাটো অসম্ভৱ বুলি অতি সহজেই সকলোৱেই বুজি উঠিছিল। সেয়েহে এই সমস্যাটো সমাধানৰ বাবে এলেন টিউৰিঙে হাতত লোৱা পন্থাটো অতি সুকীয়া আছিল। তেওঁ ভাবিছিল যে, কেৱল এটা মেছিনেহে আন এটা মেছিনক প্ৰত্যুত্তৰ দিব পাৰে। সেয়েহে, তেওঁ শিক্ষাজীৱনৰ পৰাই মনতে ভাৱি থোৱা একপ্ৰকাৰৰ `সাৰ্বজনীন' মেছিন সৃষ্টি কৰাৰ কথা ভাবিলে, যিটো মেছিনক বিভিন্ন ধৰণৰ নিৰ্দেশনা দি বিভিন্নধৰণৰ গণনা কৰোৱাব পাৰি। ইংলেণ্ডৰ ৰেডিঅ' ফেক্টৰী এটাত MI-6 ৰ সহযোগত অতি গোপনে, অশেষ পৰিশ্ৰমৰ অন্তত খ্ৰীষ্ট'ফাৰ নাম দিয়া এনে এটা যন্ত্ৰ তেওঁ গঢ়ি তুলিলে। পোনপ্ৰথমবাৰৰ বাবে অতি সৰল ৰূপৰ কম্পিউটাৰ প্ৰগ্ৰেমিঙ ব্যৱহাৰ কৰি এলেন টিউৰিঙে জাৰ্মানসকলৰ যন্ত্ৰটোৰ সঁঠিক বিন্যাসখিনি সঠিকভাৱে গণনা কৰিবলৈ সক্ষম হ'ল। এইধৰণৰ উন্নতমানৰ চোৰাংচোৱা কাৰ্য্যই অৱশেষত মিত্ৰশক্তিক দ্বিতীয় বিশ্বযুদ্ধত জয়লাভত যথেষ্টখিনি সহায় কৰিলে। এই ৰোমাঞ্চকৰ কাহিনীটোক হলিউডৰ "The Imitation Game" নামৰ চলচ্চিত্ৰখনত অতি সুন্দৰকৈ উপস্থাপন কৰা হৈছে। চলচ্চিত্ৰখনত এলেন টিউৰিঙৰ চৰিত্ৰটোত বিখ্যাত ব্ৰিটিছ অভিনেতা Benedict Cumberbatch-এ অতি নিখুঁতকৈ অভিনয় কৰিছে। এইজন এলেন টিউৰিঙৰ মনতেই মানুহৰ দৰে ভাবিব পৰা যন্ত্ৰৰ ধাৰণাটোৱে ধৰা দিছিল। অৱশ্যে দ্বিতীয় বিশ্বযুদ্ধৰ পাছতো এই `স্মাৰ্ট' যন্ত্ৰটোৰ উন্নতি সাধন কৰি থকা এলেন টিউৰিঙক ৪১ বছৰ বয়সতেই মানৱ সভ্যতাই হেৰুৱালে। সেই সময়ৰ আইন অনুসৰি সমকামী হোৱাৰ দোষত ব্ৰিটিছ চৰকাৰে তেওঁক অবৈজ্ঞানিক পদ্ধতিৰে ৰাসায়নিক দ্ৰব্যৰ সহায়ত বিষমকামীলৈ পৰিৱৰ্তন হ'বলৈ হেঁচা প্ৰয়োগ কৰিছিল। তীব্ৰ মানসিক চাপ আৰু হতাশগ্ৰস্ততাৰ ফলস্বৰূপে এলেন টিউৰিঙে ১৯৫১ চনত আত্মহত্যা কৰে। মৃত্যুৰ আগেয়ে তেওঁ পাছলৈ কৃটিম বুদ্ধিমত্তাৰ লগত জড়িত হ'ব পৰা ভালেখিনি নতুন তাত্ত্বিক ধাৰণা আগবঢ়াই থৈ গৈছিল। একবিংশ শতিকাত দৈনন্দিন জীৱনত এই ধাৰণাসমূহ ব্যৱহাৰ কৰা সমগ্ৰ মানৱ সভ্যতা এইজন গণিতজ্ঞৰ ওচৰত চিৰদিন ঋণী। অৱশেষত, ২০১৩ চনত ব্ৰিটিছ চৰকাৰৰ তৰফৰ পৰা তেওঁক মৰণোত্তৰভাৱে নিৰ্দোষী বুলি ঘোষণা কৰা হয়।
কম্পিউটাৰ এটাই শিকে কেনেকৈ?
অতি সহজ ভাষাত ক'বলৈ গ'লে, কম্পিউটাৰ এটাই নিউৰেল নেটৱৰ্ক প্ৰগ্ৰেমিং নামৰ ব্যৱস্থাটোৰে শিকাৰ পদ্ধতিটো শিশু এটাই নতুন কথা এটা শিকাৰ দৰেই। উদাহৰণস্বৰূপে, এটা শিশুক কেইবাটাও মেকুৰী আৰু কুকুৰৰ ফটো দেখুৱাই `কোনটো দেখিবলৈ কেনেকুৱা' সেয়া শিকাব পাৰি। এবাৰ শিকি লোৱাৰ পিছত শিশুটোৱে নতুন ফটো এখন দেখা পালে সেইটো কুকুৰ নে মেকুৰী সেয়া চিনাক্ত কৰিব পৰা হয়। ঠিক সেইদৰে, কম্পিউটাৰ এটাইও শিকাৰ পদ্ধতিটোৰ বাবে আগতীয়াকৈ কিছুমান তথ্য ব্যৱহাৰ কৰে, তাৰ পিছতহে ই সঠিক সিদ্ধান্ত ল'ব পৰাৰ ক্ষমতা লাভ কৰে। সেইবাবে, অনলাইন জগতখনত পৰ্য্যাপ্ত পৰিমাণৰ সময়ৰ বাবে আপোনাৰ গতিবিধি লক্ষ্য কৰাৰ পাচতহে ইউটিউব বা ফেচবুকৰ algorithmটোৱে আপোনাৰ প্ৰয়োজন/বাছনিখিনি অনুমান কৰিব পৰা হয়। এই প্ৰক্ৰিয়াটোক অধিক বিস্তাৰিত ৰূপত জানিবলৈ এটা উদাহৰণ ল'ব লাগিব। 3blue1brown নামৰ এটা ইউটিউব চেনেলত এটা বৰ সুন্দৰ উদাহৰণ আছে, সেইটোকেই যিমান পাৰি সহজকৈ ব্যাখ্যা কৰিবলৈ লৈছোঁ।
কম্পিউটাৰ এটাই হাতৰ আখৰ কিদৰে চিনাক্ত কৰে, তাৰ এটা উদাহৰণ দিওঁ। চিত্ৰ-২ত থকা সংখ্যাটোলৈ মন কৰক। এই ফটোখনৰ resolution যথেষ্ট কম হোৱা স্বত্বেও, আমাৰ মস্তিষ্কটোৱে সংখ্যাটোক ইংৰাজীৰ ৯ অংকটো বুলি চিনাক্ত কৰাত একো অসুবিধা হোৱা নাই। কিন্তু, কম্পিউটাৰ এটাই কেনেকৈ ইয়াক চিনাক্ত কৰিব? ইয়াৰ বাবে চিত্ৰটোৰ প্ৰতিটো পিক্সেলত থকা তথ্যখিনিক কম্পিউটাৰটোত ছেভ কৰিব লাগিব। প্ৰতিটো পিক্সেলৰ ক'লা/বগা ৰংটোক ০ আৰু ১ৰ মাজৰ এটা বাস্তৱ সংখ্যা হিচাপে ধৰিব পাৰি। (০ মানে সম্পূৰ্ণ ক'লা, আৰু ১ মানে সম্পূৰ্ণ বগা।) তেতিয়া ফটোখনক নম্বৰ কিছুমানৰ সংহতি হিচাপে কম্পিউটাৰটোত ৰাখিব পৰা যাব। পিছে আন এজন ব্যক্তিয়ে আকৌ সংখ্যাটো হাতেৰে লিখিলে সেই নতুন ফটোখনৰ পিক্সেলবোৰৰ তথ্যখিনি সামান্য পৰিমাণে হ'লেও সলনি হ'ব, কিয়নো হুবহু একেটা চিত্ৰকেই বাস্তৱত অঁকাটো অসম্ভৱ; আৰু কম্পিউটাৰটোৱে আগৰ পৰাই শিকি থোৱা তথ্যৰ লগত তুলনা কৰি চাই এই নতুন হাতৰ আখৰটোক চিনাক্ত কৰিব নোৱাৰিব। এইখিনিতেই নিউৰেল নেটৱৰ্কৰ প্ৰয়োজনীয়তাক বুজিব পাৰি।
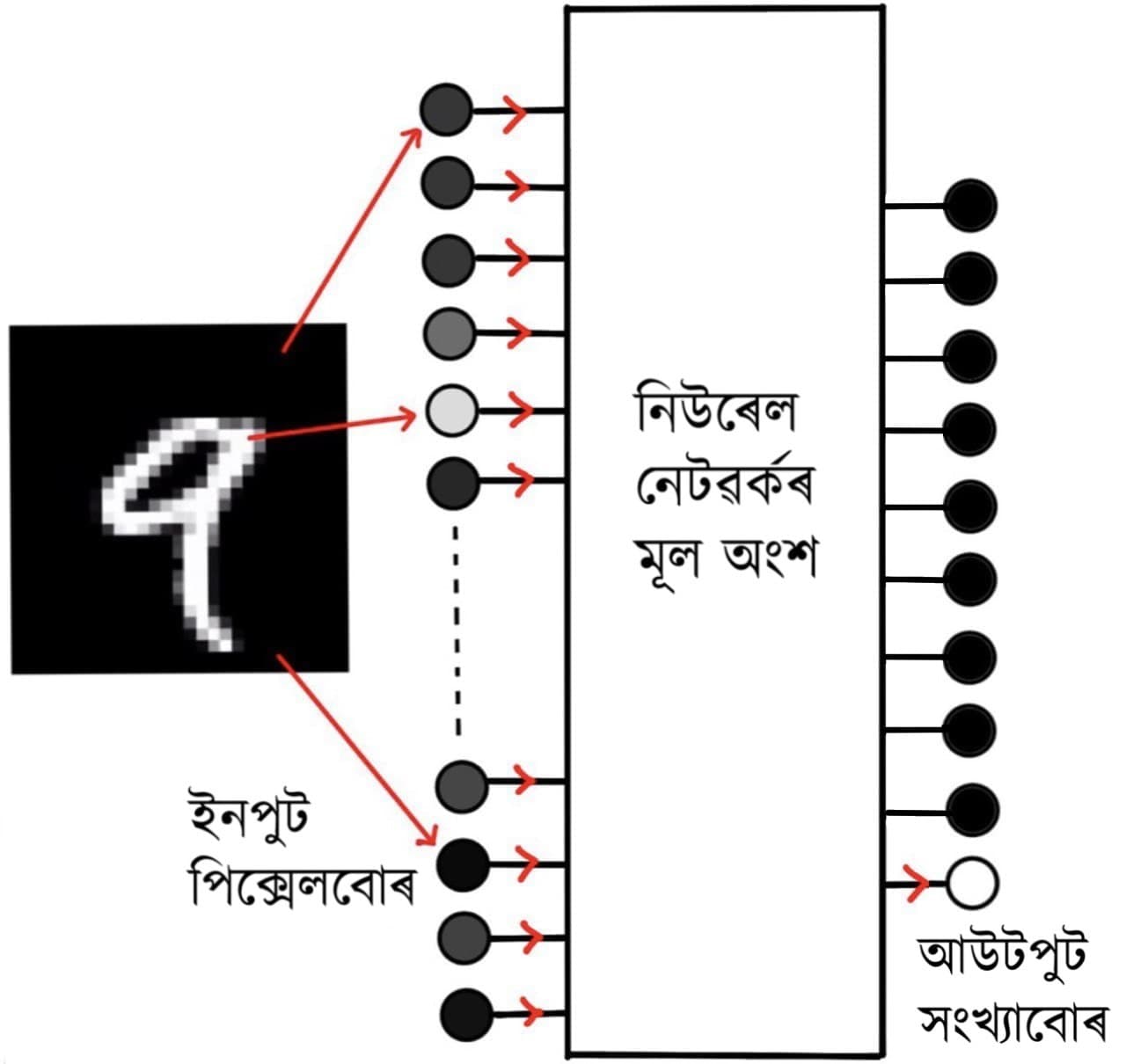
চিত্ৰ-৩ত এটা নিউৰেল নেটৱৰ্কৰ block diagram দেখুউৱা হৈছে। একেবাৰে বাওঁফালে উলম্বকৈ থকা বৃত্তকেইটাত ইনপুট চিত্ৰটোৰ প্ৰতিটো পিক্সেলৰ তথ্য সন্নিহিত হৈ আছে (০ৰ পৰা ১ৰ মাজৰ সংখ্যা হিচাপে), আৰু একেবাৰে সোঁফালৰ বৃত্তকেইটাই ০ ৰ পৰা ৯ লৈকে ইংৰাজীৰ অংককেইটাক প্ৰতিনিধিত্ব কৰিছে। মাজৰ আয়তটোত আমাৰ নিউৰেল নেটৱৰ্কটোৰ মূল আকৃতিখিনি লুকাই আছে বুলি ধৰক। ধৰা হ'ল যে এই নিউৰেল নেটৱৰ্কটোক ইতিমধ্যেই ইংৰাজীৰ অংককেইটাক চিনাক্ত কৰিবলৈ শিকোৱা হৈছে। এতিয়া, বাওঁফালে ইংৰাজীৰ ৯ৰ চিত্ৰটো ইনপুট হিচাপে দিয়াৰ লগে লগেই এটা অতি সক্ষম, আদৰ্শ নিউৰেল নেটৱৰ্কে সোঁফালৰ ৯ৰ বৃত্তটোত ১ সংখ্যাটো ৰাখিব, আৰু বাকীকেইটাত ০ সংখ্যাটো ৰাখিব। অৰ্থাৎ সমগ্ৰ নিউৰেল নেটৱৰ্কটোকেই বাওঁফালৰ চলককেইটাৰ এটা ফলন বুলি ভাবিব পাৰি। বাওঁফালে `৯ৰ নিচিনা' ইনপুট দিলে সোঁফালে ৯ৰ আউটপুটৰ ঘৰত ১ পোৱা যাব, আৰু বাওঁফালে বেলেগ এটা ইনপুট দিলে সোঁফালে সেইটো সংখ্যাৰ আউটপুটত ১ (আৰু বাকীকেইটাত ০) পোৱা যাব। নিউৰেল নেটৱৰ্কৰ সহায়ত কোনো বস্তুৰ চিনাক্তকৰণ বা কোনো সিদ্ধান্ত গ্ৰহণ ইত্যাদি কাৰ্য্য এইদৰেই কৰা হয়। এই বিশেষ ফলনটোক সঠিককৈ সৃষ্টি কৰা পৰ্য্যায়টোকেই নিউৰেল নেটৱৰ্কটোৰ `শিকাৰ পৰ্য্যায়' বুলি ক'ব পাৰি। এই শিকাৰ পৰ্যায়টোৱেই নিউৰেল নেটৱৰ্কৰ এটাৰ কাৰ্য্যপ্ৰণালীৰ অতি গুৰুত্বপূৰ্ণ পদক্ষেপ, আৰু এই পৰ্যায়টোৰ পিছতেই নিউৰেল নেটৱৰ্কটোৱে বাওঁফালে ইনপুট হিচাপে দিয়া যিকোনো এটা ইংৰাজী অংকক সোঁফালে থকা কোনো এটা অংক হিচাপে চিনাক্ত কৰিব পাৰিব। পিছে আটাইতকৈ গুৰুত্বপূৰ্ণ প্ৰশ্নটো হ'ল, সেই মাজৰ আয়তটোত কি ধৰণৰ গাঁঠনি সৃষ্টি কৰিলে এইধৰণৰ ফলাফল পোৱা যাব? ইয়াৰ উত্তৰটো অতি সৰল, আৰু সেয়েহে আচৰ্যকৰ। এইখিনিতেই শিশু এটাক কুকুৰ বা মেকুৰীৰ ফটো দেখুৱাই সিহঁতক চিনাক্ত কৰিবলৈ শিকোৱাৰ উপমাটো প্ৰাসংগিক হৈ পৰে। এই প্ৰক্ৰিয়াটো বৰ্ণনা কৰাৰ আগেয়ে নিউৰেল নেটৱৰ্কৰ লগত জড়িত শব্দ কিছুমানৰ লগত চিনাকি হৈ ল'লে পিছৰখিনি কথা বুজিবলৈ সুবিধা হ'ব।
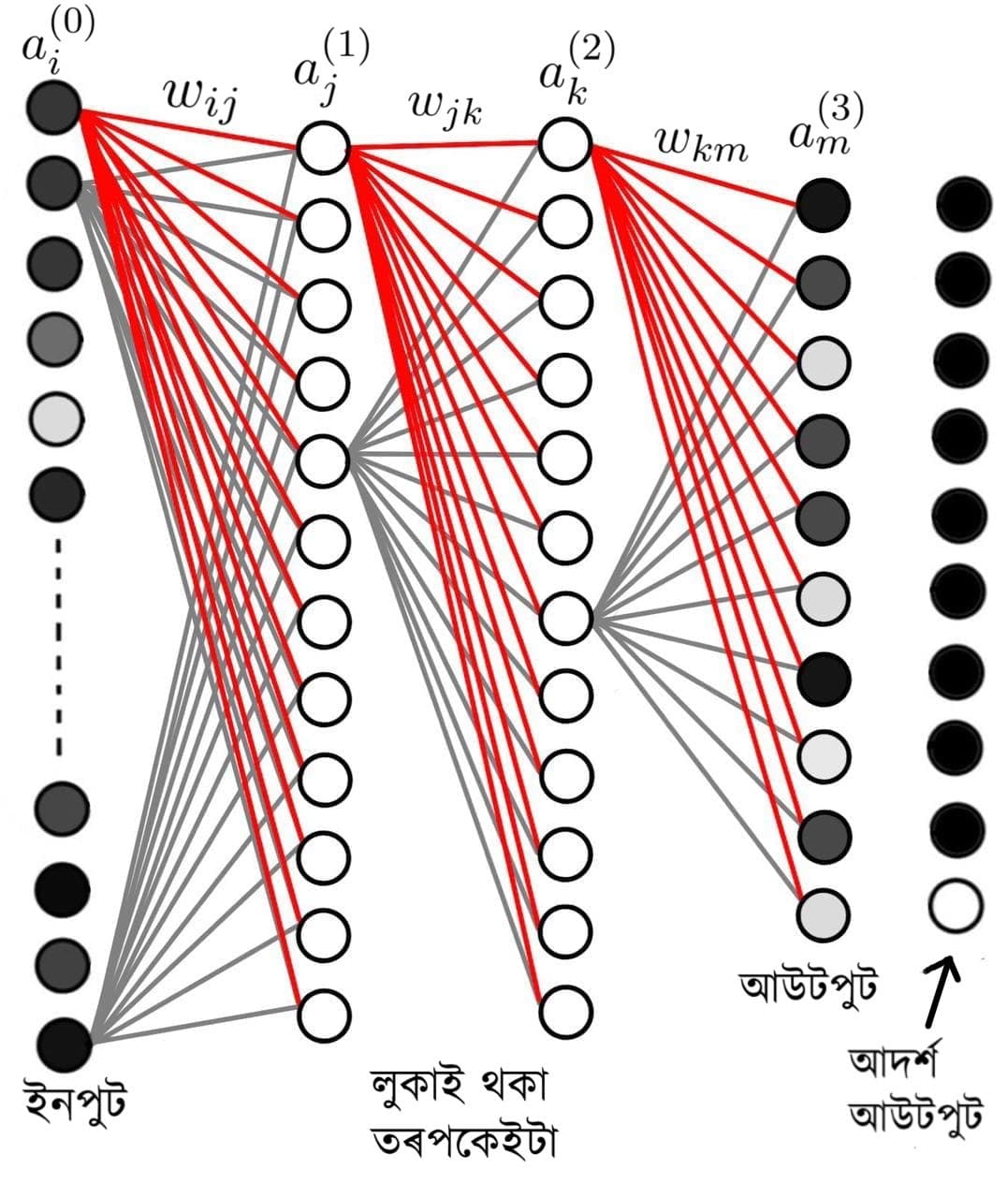
নিউৰেল নেটৱৰ্কৰ লগত জড়িত অংশ কিছুমানক ইচ্ছাকৃতভাৱেই মানৱ মস্তিষ্কৰ লগত জড়িত শব্দ কিছুমানেৰে নাম দিয়া হৈছে। ব্লক চিত্ৰটোৰ নম্বৰ ধৰি ৰখা বৃত্তকেইটাক নিউৰণ (স্নায়ুকোষ) বুলি কোৱা হয়। মানুহৰ স্নায়ুকোষে যিদৰে ইলেক্ট্ৰনিক তথ্য ধৰি ৰাখিব পাৰে, ঠিক সেইদৰে এই বৃত্তকেইটাও তথ্য (সংখ্যা) ধৰি ৰাখে। উলম্বকৈ শাৰী পাতি থকা নিউৰণবোৰৰ সমষ্টিক এটা `তৰপ' (layer) বুলি কোৱা হয়। এটা তৰপৰ নিউৰণ আৰু কাষতেই থকা আন এটা তৰপৰ নিউৰণবিলাক ইটোৱে সিটোৰ লগত গাণিতিক নিয়মেৰে সংলগ্ন হৈ থাকে, ঠিক মস্তিষ্কৰ স্নায়ুবোৰৰ মাজৰ সংযোগবোৰৰ দৰেই। এটা নিউৰণত থকা সংখ্যাটোৱে কাষৰ তৰপটোত থকা নিউৰণবোৰৰ সংখ্যাক নিৰ্ধাৰণ কৰে। ঠিক সেইদৰে, নিউৰণটোত থকা সংখ্যাটোৰ মানৰ ওপৰত ভিত্তি কৰি নিউৰণটো সক্ৰিয় বা নিষ্ক্ৰিয় হ'ব পাৰে। সক্ৰিয় নিউৰণবোৰে কাষৰ তৰপৰ নিউৰণবোৰক প্ৰভাৱিত কৰিব পাৰে, আৰু নিষ্ক্ৰিয়বোৰে নোৱাৰে। এতিয়া, আমি নিউৰেল নেটৱৰ্কটোৰ সম্পূৰ্ণ গাঁঠনিটো চিত্ৰ-৪ত দিয়াধৰণে প্ৰকাশ কৰিব পাৰোঁ। নিউৰেল নেটৱৰ্কটোৰ মূল অংশটোও কিছুমান নিউৰণৰ তৰপেৰেই গঠিত। ইয়াৰ প্ৰতিটো নিউৰণেই কাষৰ তৰপকেইটাৰ প্ৰতিটো নিউৰণৰ লগত সংলগ্ন হৈ থাকে যদিও, চিত্ৰটো সৰল কৰি ৰাখিবলৈ ইয়াত কেইটামান সংযোগহে দেখুউৱা হৈছে। একেবাৰে বাওঁফালে থকা ইনপুট সংখ্যাকেইটাক \( a^{(0)}_i \) চিহ্নটোৰে প্ৰকাশ কৰা হৈছে, আৰু এইকেইটাক এটা column matrix হিচাপে প্ৰকাশ কৰিব পাৰি। এই আটাইকেইটা সংখ্যাৰ মান হৈছে ইনপুট সংখ্যাকেইটা। ঠিক সেইদৰে, পৰৱৰ্তী তৰপটোত থকা \( a^{(1)}_j \) সংখ্যাকেইটাকো এটা column matrix হিচাপে প্ৰকাশ কৰিব পাৰি। সদ্যহতে আমি এই দ্বিতীয় তৰপটোৰ সংখ্যাকেইটা নাজানো যদিও, এইকেইটাক প্ৰথম তৰপটোৰ ইনপুট সংখ্যাবোৰৰ ৰৈখিক যোগফল হিচাপে প্ৰকাশ কৰা হয়। এই গাণিতিক নিয়মটো এনেধৰণৰ। \[ a^{(1)}_j = \sum w_{ij} a^{(0)}_i \] অৰ্থাৎ, \( w_{ij} \) মেট্ৰিক্সটোৱে প্ৰথম শাৰী নম্বৰৰ লগত দ্বিতীয় শাৰী নম্বৰক সংযোগ কৰিছে। সদ্যহতে এই \( w_{ij} \) সংখ্যাকেইটাৰ মান আমি নাজানো যদিও প্ৰাৰম্ভিক অৱস্থাত এইকেইটাক যাদৃচ্ছিক মান দিয়া হয়। `ওজন' নাম দিয়া এই মেট্ৰিক্সৰ সংখ্যাকেইটায়েই হৈছে শিকা প্ৰক্ৰিয়াটোৰ আটাইতকৈ গুৰুত্বপূৰ্ণ অংশ। এই একেই পদ্ধতিৰেই নিউৰেল নেটৱৰ্কটোৰ প্ৰতিটো তৰপ ইয়াৰ কাষৰ তৰপকেইটাৰ লগত সংলগ্ন হৈ থাকে। এই আটাইবোৰ নিউৰণেই এইদৰে গাণিতিক নিয়মেৰে সংলগ্ন হৈ এখন বৃহৎ, জটিল জালিকাৰ সৃষ্টি কৰে। এই জালিকাখন মানৱ মস্তিষ্কৰ স্নায়ুকোষ বিলাকে পৰস্পৰৰ লগত সংলগ্ন হৈ সৃষ্টি কৰা জালিকাখনৰ দৰেই। এই বৈশিষ্ট্যটোৰ বাবেই এই প্ৰগ্ৰেমিং পদ্ধতিটোক নিউৰেল নেটৱৰ্ক (অৰ্থাৎ স্নায়ু-জালিকা) বুলি কোৱা হয়।
এতিয়া, এই নিউৰেল নেটৱৰ্কটোৱে ইংৰাজীৰ ৯ অংকটো চিনাক্ত কৰিবলৈ কেনেকৈ শিকিব সেয়া কওঁ। আৰম্ভণিতেই ৯ অংকটোৰ লগত জড়িত ইনপুট সংখ্যাকেইটাই দ্বিতীয় তৰপটোত কিছুমান যাদৃচ্ছিক সংখ্যাৰ সৃষ্টি কৰিব (কিয়নো, \( w_{ij} \) কেইটাৰ মান যাদৃচ্ছিক)। সেই দ্বিতীয় তৰপটোৰ সংখ্যাকেইটাই একেদৰেই তৃতীয় তৰপটোতো কিছুমান যাদৃচ্ছিক সংখ্যা সৃষ্টি কৰিব, আৰু একেদৰেই, আউটপুট তৰপটোতো যাদৃচ্ছিক সংখ্যা কিছুমান পোৱা যাব। পিছে, আমি ইতিমধ্যেই জানো যে আউটপুট তৰপটোৰ সংখ্যাসমূহ কেনেধৰণৰ হ'ব লাগে (চিত্ৰ-৪ৰ একেবাৰে সোঁফালে উলম্বকৈ থকা বৃত্তকেইটাৰ দৰে)। সেয়েহে, আউটপুটৰ সংখ্যাকেইটাৰ লগত এই প্ৰত্যাশিত সংখ্যাকেইটাৰ পাৰ্থক্যৰ মান হিচাপ কৰা হয়। এই পাৰ্থক্যৰ ফলনটোক cost function বুলি কোৱা হয়। কম্পিউটাৰটোক সেই ওজনকেইটাৰ মান সালসলনি কৰিবলৈ নিৰ্দেশ দিয়া হয়, যাতে সেই নিৰ্দিষ্ট ইনপুটটোৰ বাবে cost functionটোৰ মান নুন্যতম হয়, আৰু আউটপুটৰ সংখ্যাখিনিৰ মান প্ৰত্যাশিত মানখিনিৰ ওচৰ চাপে। এই নতুন ওজনকেইটাৰ মান নিৰ্দিষ্ট কৰি নিউৰেল নেটৱৰ্কটোত ছেভ কৰি ৰখা হয়। ঠিক সেইদৰে, পুনৰবাৰ আন এজন ব্যক্তিৰ হাতৰ আখৰেৰে লিখা ৯ অংকটোৰ বাবে একেদৰেই আউটপুটৰ লগত প্ৰত্যাশিত মানবোৰৰ তাৰতম্য হিচাপ কৰি পুনৰ ওজনবোৰৰ মান সালসলনি কৰা হয়, আৰু cost functionটোৰ মান নুন্যতম কৰিবলৈ চেষ্টা কৰা হয়। এইদৰেই আটাইকেইটা ইংৰাজী অংকৰ বাবে এই প্ৰক্ৰিয়াটোৰ পুনৰাবৃত্তি কৰি থাকিলে সেই ওজনবিলাকে অৱশেষত এক সৰ্বোত্তম মান লয়, আৰু তেতিয়াই নিউৰেল নেটৱৰ্কটোৱে অংককেইটাক চিনাক্ত কৰিবলৈ শিকিলে বুলি ক'ব পাৰি। এতিয়া এই নিউৰেল নেটৱৰ্কটোক নতুনকৈ হাতে লিখা এটা ইংৰাজীৰ অংক পঢ়িবলৈ দিলে, ই সোঁফালৰ সেই নিৰ্দিষ্ট সংখ্যাটোক প্ৰতিনিধিত্ব কৰা নিউৰণটোত ১ৰ ওচৰৰ মান এটা সৃষ্টি কৰিব, আৰু বাকীকেইটাত ০ৰ ওচৰৰ মান সৃষ্টি কৰিব।
মন কৰিব, যে \( w_{ij} \) মানটোৱে প্ৰথম শাৰীৰ \( i \)-নং নিউৰণটোৰ লগত পিছৰ শাৰীৰ \( j \)-নং নিউৰণটোৰ মানক সংযোগ কৰিছে। এইটোৰ মান যিমানেই ডাঙৰ হয়, সিমানেই \( i \) আৰু \( j \)-নং নিউৰণ দুটাৰ মাজৰ নিৰ্ভৰশীলতাৰ মান অধিক হয়। এই কথাটো মানৱ মস্তিষ্কৰ স্নায়ুবিলাকৰ সংযোগবোৰৰ দৰেই। মানুহ এজনে নতুন কথা এটা শিকিলে সেই নিৰ্দিষ্ট কথাটোৰ লগত জড়িত স্নায়ুবিলাকৰ মাজৰ সংযোগবোৰ অধিক শক্তিশালী হৈ পৰে। কেইটামান সৰল গাণিতিক নিয়মে কিদৰে এই অত্যন্ত জটিল পৰিঘটনাটোক নকল কৰিব পাৰে, সেয়া অতি আকৰ্ষণীয় বিষয়।
এইখিনিতেই আন কেইটামান প্ৰায়োগিক তথ্য উল্লেখ কৰিব পাৰি। আউটপুটৰ তথ্যখিনিৰ পৰা cost functionটো হিচাপ কৰি ইয়াৰ নুন্যতম মানৰ বাবে বিভিন্নধৰণৰ ওজনবিলাকৰ মান নিৰ্ণয় কৰা পদ্ধতিটোক back propagation algorithm বুলি কোৱা হয়। এই পদ্ধতিটো differential calculusৰ সহায়ত কোনো এটা ফলনৰ নুন্যতম মান নিৰ্ণয় কৰাৰ দৰেই। এটা তৰপৰ পৰা আন এটা তৰপৰ সংখ্যা সৃষ্টি কৰা সমীকৰণটোত বিভিন্ন কাৰিকৰী কাৰণত ওজনকেইটাৰ উপৰিও আন কিছুমান প্ৰাচল ( \( B_i \)) ব্যৱহাৰ কৰা হয়। এইবিলাক প্ৰাচলৰ মানো সেই একেই পদ্ধতিৰেই নিৰ্ণয় কৰা হয়। তদুপৰি নিৰ্দিষ্ট নিউৰণ এটা সক্ৰিয় নে নিষ্ক্ৰিয় হ'ব সেয়া নিৰ্ণয় কৰিবলৈ সেই মূল সমীকৰণৰ মানটোক activation (\( \delta \)) নামৰ আন এটা ফলনৰ সহায়ত নিৰ্ণয় কৰা হয়। এই ফলনটোৱে সেই নিউৰণটোৰ কোনো নুন্যতম মানৰ বাবেহে নিউৰণটোক সক্ৰিয় কৰি ৰাখে। সেই নুন্যতম মানতকৈ কম মান থকা নিউৰণবোৰৰ মান বলপূৰ্বকভাৱে শূণ্য কৰা হয়, আৰু তেতিয়া সেই নিউৰণটোৱে পৰৱৰ্তী তৰপটোৰ মানবিলাকক প্ৰভাৱিত কৰিব নোৱাৰে। এইখিনি পৰিৱৰ্তনেৰে সৈতে ১-নং সমীকৰণটোৱে তলত দিয়াৰ দৰে ৰূপ লয়। \[ a^{(1)}_j = \delta\left\{ \sum\limits_i (w_{ij} a^{(0)}_i + B_i) \right\} \] অৱশ্যে এই নতুন পৰিৱৰ্তনখিনিৰ অবিহনেও নিউৰেল নেটৱৰ্কটোৰ কাৰ্য্যপ্ৰণালী বুজিব পাৰি। এই পৰিৱৰ্তনখিনি প্ৰকৃততে নেটৱৰ্কটোৰ দক্ষতা বৃদ্ধি কৰিবলৈ ব্যৱহাৰ কৰা হয়। আমি আলোচনা কৰা উদাহৰণটোত ইনপুট আৰু আউটপুটৰ মাজত ১২ টাকৈ নিউৰণ-যুক্ত দুটা তৰপ দেখুউৱা হৈছে যদিও, বাস্তৱত কম্পিউটাৰটোৰ কাৰ্য্যক্ষমতাৰ ওপৰত নিৰ্ভৰ কৰি যিকোনো সংখ্যাৰ নিউৰণৰ সৈতে কেইবাটাও তৰপ ব্যৱহাৰ কৰিব পাৰি। আটাইতকৈ আমোদজনক কথাটো হ'ল যে, এজন কম্পিউটাৰ প্ৰগ্ৰেমাৰে এইবিলাক তথ্য নজনাকৈও অতি সহজে নিউৰেল নেটৱৰ্ক ব্যৱহাৰ কৰিব পাৰে। উদাহৰণস্বৰূপে, পাইথন (Python) নামৰ প্ৰগ্ৰেমিং ভাষাটোৰ সহায়ত টেনছৰ-ফ্ল' (TensorFlow), পাই-টৰ্চ (PyTorch) আদিৰ দৰে বিভিন্ন লাইব্ৰেৰী ব্যৱহাৰ কৰি সহজে ইনপুট ডাটাৰ পৰা আউটপুট ডাটা সৃষ্টি কৰিব পাৰি। নিউৰেল নেটৱৰ্কটোৱে ইনপুট ডাটাখিনিৰ পৰা কিদৰে তথ্য সংগ্ৰহ কৰি ব্যৱহাৰ কৰিব সেই সকলোবোৰ নিৰ্দেশ এই লাইব্ৰেৰীবোৰত ইতিমধ্যে উপলব্ধ কৰা হৈছে। সেই আটাইখিনি প্ৰগ্ৰেম নিজেই লিখাৰ কোনো প্ৰয়োজন নাই।
আমাৰ চাৰিওফালৰ নিউৰেল নেটৱৰ্কবোৰ
এতিয়া বৰ্ণনা কৰি থকা নিউৰেল নেটৱৰ্কটো এটা অতি সৰল আৰু সাধাৰণ উদাহৰণহে। নিউৰেল নেটৱৰ্কবোৰক দৈনন্দিন জীৱনৰ অতি সাধাৰণ সমস্যাবোৰৰ পৰা বিজ্ঞান আৰু প্ৰযুক্তিবিদ্যাৰ জগতৰ অতি জটিল সমস্যাবোৰলৈকে সমাধান কৰিবলৈ দিয়া হয়। সহজ সৰল ৰূপত মানুহে লিখা কম্পিউটাৰ প্ৰগ্ৰাম বিলাক প্ৰকৃততে কিছুমান চিধা নিৰ্দেশহে। ইয়াৰ তুলনাত নিউৰেল নেটৱৰ্কবোৰৰ কাৰ্য্যক্ষমতা সাংঘাটিক বেছি। উদাহৰণস্বৰূপে, এতিয়ালৈকে ইউৰোপৰ CERNত থকা LHC নামৰ কণাত্বৰক যন্ত্ৰটোৰ লগত জড়িত CMS নামৰ ডিটেক্টৰটোত চিধা নিৰ্দেশ কিছুমানৰ সহায়ত ডিটেক্টৰটোত উপ-পাৰমাণৱিক কণাই সৃষ্টি কৰা বিভিন্ন ধৰণৰ বৈদ্যুতিক সংকেত সমূহক বিভিন্নধৰণৰ কণা হিচাপে চিনাক্ত কৰি অহা হৈছিল। অৰ্থাৎ, সৰল ভাষাত ক'বলৈ হ'লে, সেই সংকেত সমূহৰ লগত জড়িত সংখ্যাসমূহে কিছুমান নিৰ্দিষ্ট "If condition" মানি চলিলে সেই সংকেত সমূহক কোনো এটা কণা বুলি চিনাক্ত কৰা হৈছিল। ২০২২ চনৰ পৰা আকৌ LHCত কণাত্বৰণ প্ৰক্ৰিয়াটো তৃতীয় বাৰৰ বাবে আৰম্ভ কৰা হ'ব। এইবাৰ কণাসমূহক অধিক সক্ষমতাৰে চিনাক্ত কৰিবলৈ নিউৰেল নেটৱৰ্কৰ সহায় লোৱা হ'ব। IISER-Puneৰ পৰীক্ষামূলক কণা পদাৰ্থবিজ্ঞানৰ বিভাগটোৰ পৰা আমিও সেই গৱেষণাৰ লগত জড়িত হৈ আছো, আৰু মই সদ্যহতে পোহৰৰ কণাবিধক চিনাক্ত কৰাৰ বাবে এটা নিউৰেল নেটৱৰ্ক সৃষ্টি কৰিবলৈ চেষ্টা চলাই আছোঁ। তাৰ বাহিৰেও, মোৰ দৈনন্দিন জীৱনটো নিউৰেল নেটৱৰ্ক অবিহনে অসম্পূৰ্ণ। ফোনটো আনলক কৰিবলৈ মোৰ হাতৰ চাপটোক চিনাক্ত কৰা পদ্ধতিটো একেই। সদ্যহতে এই কথাখিনি টাইপ কৰি থাকোঁতেও মোৰ key-board খনে পৰৱৰ্তী শব্দটো কি হ'ব সেয়া অনুমান কৰিব পাৰিছে। মোৰ অনলাইন খোৱাবস্তু অৰ্ডাৰ দিয়া এপটোৱে মই কিধৰণৰ খাদ্য খাই ভাল পাওঁ সেয়া জানে। এই সকলোবোৰ কেইটামান সাধাৰণ গণিতৰ নিয়মক অতি কৌশলীভাৱে ব্যৱহাৰ কৰাৰ ফল! মানুহৰ দৰেই অনুভৱ কৰিব পৰা, সুখ-দুখ প্ৰকাশ কৰিব পৰা, আৰ্থাৰ ছি ক্লাৰ্ক বা এলেন টিউৰিঙৰ সপোনৰ মেছিনবিলাকক এতিয়ালৈকে পিছে সৃষ্টি কৰা হোৱা নাই। কিন্তু যোৱা ৫০ বছৰৰ পৰা আৰম্ভ কৰি বৰ্তমানৰ এলেক্সা, ছিৰি আদিৰ দৰে কম্পিউটাৰ প্ৰগ্ৰামবোৰৰ ইতিহাস অধ্যয়ন কৰিলে সেই সপোনবোৰ সঁচা হ'বলৈ বেছি দিন নালাগিব যেন অনুভৱ হয়।